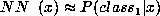 and
and
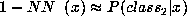 .
. 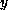 is now either equal to one
or zero. We obtain
is now either equal to one
or zero. We obtain
If we assume an additive noise model, we can again use the same update
rules as in regression. Often it is preferable to use the cross-entropy
as a log-likelihood function. We only consider the 2-class problem
such that 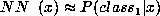 and
and
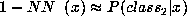 .
. 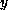 is now either equal to one
or zero. We obtain
is now either equal to one
or zero. We obtain
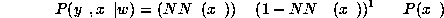
and for missing data
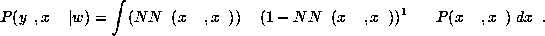
We obtain for a compete pattern
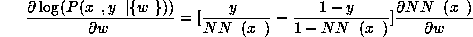
and for an incomplete pattern
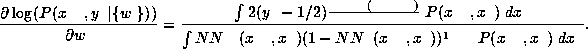
This equation looks more formidable than it really is if one realizes that
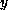 is either zero or one.
Using the approximation for the density, we obtain
is either zero or one.
Using the approximation for the density, we obtain
if 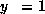

if 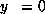
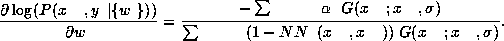
with
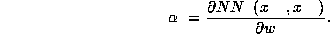
XXXXXXXXX
As an example, a network trained for economical predictions should not become useless if one of the indicator variabled becomes unavailable or useless because of economical or political changes. Rather we could consider them as unavailable information. Similarly, in control applications it might not be necessary to stop a production line simply because a sensor had failed: the information that the failing sensor delivers might be also contained in the measurements of other sensors, although this relationship might not be clear or obvious.
For the log-likelihood we really need the logarithm of this
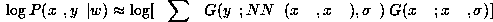
such the gradient becomes