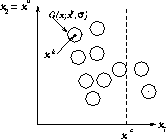
Figure: The circles indicate 10 Gaussians approximating the input density distribution.
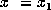 indicates the known input,
indicates the known input,
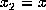 is unknown.
is unknown.
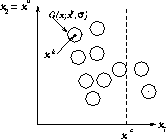
Figure: The circles indicate 10 Gaussians approximating the input density distribution. 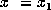 indicates the known input,
indicates the known input,
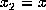 is unknown.
is unknown.
We assume that a neural network 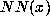 has been trained to predict
has been trained to predict
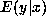 , the expectation of
, the expectation of 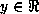 given
given 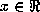 .
During recall we would like
to know the network's prediction based on an incomplete input vector
.
During recall we would like
to know the network's prediction based on an incomplete input vector
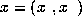 where
where  denotes the known inputs and
denotes the known inputs and
 the unknown inputs.
The optimal prediction given the known features can be written as
(Ahmad and Tresp, 1993)
the unknown inputs.
The optimal prediction given the known features can be written as
(Ahmad and Tresp, 1993)
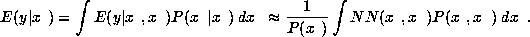
Similarly, for a network trained to estimate class probabilities,
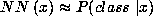 ,
simply substitute
,
simply substitute 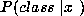 for
for 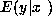 and
and
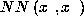 for
for 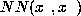 in the last equation.
in the last equation.
The integrals in the last equations can be problematic. In the worst case they have to be approximated numerically (Tresp, Ahmad and Neuneier, 1994) which is costly, since the computation is exponential in the number of missing inputs. For networks of normalized Gaussians, there exist closed form solutions to the integrals (Ahmad and Tresp, 1993). The following section shows how to efficiently approximate the integral for a large class of algorithms.